| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 이산형 확률분포
- 주식데이터시각화
- 콕스비례모형
- R ggplot2
- dplyr
- CrossValidation
- R 결측치
- 강화학습 #추천서적 #강화학습인액션
- 미국 선거데이터
- geom_errorbar
- 데이터 핸들링
- R 연습문제
- 확률실험
- R
- ggplot2
- 의사결정나무
- Bias-Variance Tradeoff
- 생존그래프
- 교차타당성
- ISLR
- R filter
- ggplot()
- 카플란마이어
- ggsurvplot
- R select
- 생존분석
- R dplyr
- 데이터핸들링
- R mutate
- R문법
- Today
- Total
Must Learning With Statistics
12. 범주형 자료분석 본문

Chapter12. 범주형 자료분석
범주형 자료분석은 변수들이 이산형 변수일 때 주로 사용하는 분석입니다. 예를 들어, 두 제품 간의 선호도가 성별에 따라 연관이 있는지 여부를 판단하고자 하는 경우, 각 집단 간의 비율차이가 있는지 확인하기 위한 경우 등에 주로 사용합니다.
범주형 변수를 다룰 때에는 일반적으로 그 빈도를 세서 표를 작성하게 됩니다. 만약 두 변수의 범주가 교차되어 있다면 이 표를 분할표(contingency table)라고 부릅니다. 사실 범주형 변수를 요약하는 방법은 이러한 분할표 말고는 적당한 것이 없습니다. 분할표를 통해서 범주 별 비교를 하고 분할표를 기반으로 범주형 변수의 독립성, 동질성 검정 등의 카이제곱 검정을 하게 됩니다. 그만큼 분할표는 쉽지만 중요한 개념이며 로지스틱 회귀모형 등으로 대표되는 일반화 선형모형을 해석하는 과정에서도 사용됩니다.
1. 비율의 비교
2x2 분할표를 통한 비율의 비교에 대해 다뤄보겠습니다. 두 범주형 변수 모두 두 가지 범주만을 갖는 이항변수일 때, 각 범주의 빈도를 이용해 2x2 분할표를 작성할 수 있으며, 이 분할표를 이용하면 여러 가지 방법의 범주별 비교를 할 수 있습니다. 예를 들어 단순하게 빈도의 크기를 비교할 수가 있고 한 변수의 각 범주 별 다른 변수의 비율을 비교할 수도 있습니다.
우리는 이 중 대표적으로 상대위험도와 오즈비라는 두 개의 비율 비교 척도를 다룰 것이며 이 두 척도는 범주형 변수를 분석할 때 언제나 언급되는 스테디 셀러입니다.
상대위험도(relative risk)
흔히 r.r 이라 불리는 상대위험도는 한 변수의 범주 별 다른 변수의 비율을 상대적으로 비교할 때 쓰이며 첫 범주에 속할 확률 추정량과 두 번째 범주애 속할 확률 추정량의 비로 정의됩니다. 또한 확률은 각 범주의 비율로 추정됩니다.
예를 들어 첫 번째 변수 \(Y\)가 어떤 시험의 결과(PASS, FAIL)이고 하고 두 번째 변수 \(X\)가 학력(고졸, 대졸)이라고 했을 때 다음과 같은 표를 작성할 수 있습니다.

- 대졸 중 시험에 합격한 비율은 \(\frac{30}{50}\)입니다.
- 고졸 중 시험에 합격한 비율은 \(\frac{15}{40}\)입니다.
- 두 그룹의 상대위헙도 추정량(\(\widehat {r.r}\))은 \(\frac {30} { 50} / \frac {15} {40}\) 로 1.6입니다.
해석을 하면 대졸의 경우가 고졸의 경우보다 시험에 합격한 비율이 60% 높다는 것을 알 수 있으며, 추정의 관점에서 해석하면 대졸자의 합격 확률이 고졸의 1.6배라고 볼 수 있습니다. 또한 상대위험도가 1에 가까울수록 두 변수사이에 연관성이 없다는 뜻이며 0에 가까워지거나 커질수록 음 혹은 양의 관계를 갖는다는 의미입니다. 상대위험도는 매우 직관적인 비교 지표로 누구나 쉽게 구할 수 있고 쉽게 해석할 수 있다는 큰 장점이 있습니다.
오즈비(odds ratio)
상대위험도와 더불어 두 범주형 변수의 범주 별 비교에 자주 사용되는 척도로 오즈비라는 것이 있습니다. 오즈비는 오즈(성공확률/실패확률)의 각 범주 별 비로 정의되며 상대위험도보다 조금 더 유연한 특징을 보입니다. 성공확률(관심 범주에 속할 확률)을 \(\pi\)라고 했을 때 오즈와 오즈비는 다음과 같이 표현할 수 있습니다.
\[ odds = \frac {\pi} {1-\pi}\\ \]
\[ \quad \\ o.r = \left( \frac { \pi_1} {1-\pi_1} \right) / \left( \frac { \pi_2} {1-\pi_2} \right) \]
상대위험도는 매우 직관적은 척도지만 한 변수의 수를 고정시킨 조사에서는 사용이 불가능하다는 단점이 있습니다. 오즈비는 이러한 경우에도 문제 없이 사용될 수 있으며 대칭적으로 구해지기 때문에 반응변수와 설명변수의 구별 없이 같은 값을 제시해 줍니다. 예를 통해 확인하겠습니다.

알콜중독과 심장질환의 연관성을 보기 위하여 심장질환을 갖고 있는 사람과 그렇지 않은 사람을 각각 50명, 100명씩 선정하여 알콜중독 여부와 비교한다고 했을 때, 분석자는 상대위험도를 사용할 수 없습니다. 각 관측치가 독립적으로 랜덤하게 선택된 것이 아니고 심장질환 여부에 의해 정해진 비율 혹은 숫자에 따라 선정된 집단이기 때문입니다. 단적으로 전체 표본 중 심장질환자의 비율이 \(\frac 1 3\) 인 것은 미리 그렇게 정해 놓았기 때문이지, 실제로 3명 중 1명이 심장질환을 가지고 있다는 의미가 아닙니다. 이러한 경우 추정된 확률은 의미가 없게되고 추정된 확률의 비를 이용하는 상대위험도 역시 의미를 잃게 됩니다. 그렇지만 오즈비는 이러한 제약에 유연합니다.
- 알콜중독자 중 심장질환의 추정된 오즈\((\widehat {odds}_{x=1})\) 는 \(\frac {4/6} {2/6} = \frac 4 2\)입니다.
- 비알콜중독자 중 심장질환의 추정된 오즈( \(\widehat {odds}{x=0}\))는 \(\frac { 46/144 } {98/144} = \frac {46} {98}\) 입니다.
- 오즈비 (\(\widehat {o.r}\))는 \(\frac {\widehat {odds}{x=1}} {\widehat {odds}{x=0}}\) = \(\frac { 4/2 } { 46/98} = \frac {98} {23}\)입니다.
심장질환이 있을 오즈는 알콜중독자 집단이 비중독자 집단의 약 4.26배인 것을 알 수 있습니다. 우리에게 익숙한 확률에 대한 지표가 아닌 오즈라는 생소한 척도를 이용해서 조금 낯설 수는 있으나 오즈비는 분할표에서 자주 사용되는 것은 물론이고 확률을 선형화하는 여러 통계 모형에서 사용되므로 익숙해질 필요가 있습니다. 상대위험도와 마찬가지로 두 변수가 연관이 없다면 오즈비는 1에 가까울 것이며 0에 가까워지거나 커질수록 밀접한 연관성을 보입니다. 또한 실패에 대한 오즈비는 성공에 대한 오즈비의 역수로 표현되며 같은 연관도를 나타냅니다. 즉, 심장질환이 있을 오즈가 아닌 심장질환이 없을 오즈를 이용하여 오즈비를 구하면 4.26의 역수인 0.2346이 나올 것이고 이는 같은 수준의 연관성을 의미합니다.
2. 카이제곱 독립성 검정
카이제곱 독립성 검정은 두 범주형 변수가 독립적으로 분포하는지를 테스트하는 검정입니다. 이 역시 분할표에서 진행되며 일반적으로 2x2가 아닌 여러 범주를 갖고 있는 경우에 사용합니다.
카이제곱 독립성 검정의 기본적 아이디어는 관측빈도와 기대빈도(두 변수가 독립일 때의 빈도)의 차이를 비교하는 것입니다. 이 방법론을 자세히 살펴보면 다음과 같습니다.
각 범주(셀)의 기대빈도가 높다면(일반적으로 5를 기준으로 합니다), 정규분포 근사를 할 수 있습니다.
정규 근사가 가능하면 이를 이용해 카이제곱 통계량을 얻을 수 있습니다. (5장 참고)
이 카이제곱 통계량은 관측빈도와 기대빈도 차이의 변동을 정량화한 통계량입니다.
카이제곱 통계량이 충분히 높다면 관측빈도와 기대빈도의 차이는 크다고 할 수 있습니다.
만약 관측빈도와 기대빈도의 차이가 충분히 크면, 두 변수가 독립적이지 않다는 결론을 내리게 됩니다.
예를 하나 보겠습니다.

기대빈도는 두 변수가 통계적으로 독립이라는 귀무가설(\(H_0\)) 하에 기대되는 빈도이고 이 귀무가설을 다른 방식으로 표현하면 \(H_0 : \pi_{ij} = \pi_{i\cdot} \; \cdot\; \pi_{\cdot j}\)입니다. 위의 표를 이용하여 이 아이디어를 생각해봅시다.
- \(\pi_{ij}\)는 각 셀에 속할 확률입니다. 예를 들어 지역3이면서 B당을 지지할 확률은 \(\pi_{23}\)이 됩니다.
- \(\pi_{i \cdot}\)은 i번 째 행에 속할 확률로 B당을 지지할 확률은 \(\pi_{2\cdot}\)입니다.
- \(\pi_{\cdot j}\)는 j째 열에 속할 확률입니다. 지역3에 속할 확률은 \(\pi_{\cdot 3}\) 입니다.
만약 두 변수가 전혀 연관이 없다면 확률의 곱법칙에 의해 지역3에 속하면서 B당을 지지할 확률은 지역 3에 속할 확률과 B당을 지지할 확률의 곱으로 표현될 것입니다. 그렇기 때문에 두 변수가 통계적으로 독립이라는 것은 \(\pi_{ij} = \pi_{i\cdot} \; \cdot\; \pi_{\cdot j}\) 과 동치입니다. 또한 \(\pi_{i\cdot }\)은 \(\frac{n_{i\cdot}}{n}\) 으로 추정되고 \(\pi_{\cdot j}\)는 \(\frac{n_{\cdot j}}{n}\)은 으로 추정됩니다. 즉, 각 행과 열의 빈도와 전체빈도의 비율로 추정되는 것으로 볼 수 있습니다.
기대빈도를 구하는 방법은 다음과 같습니다. \[ E_{ij} = n \cdot \pi_{ij} = n\cdot \pi_{i \cdot} \cdot \pi_{\cdot j}\\ \;\\ (추정)\Rightarrow n\cdot \left( \frac {n_{i\cdot}} {n} \right)\cdot \left( \frac {n_{\cdot j}} {n} \right) = \frac {n_{i\cdot}\cdot n_{\cdot j} }{n} \]
이를 이용해 지역3에 속하면서 B당을 지지할 기대빈도를 구해보면 약 161.44가 나옵니다. 이런식으로 각 셀에 대한 기대빈도를 구해 괄호로 표현하면 다음과 같고 각 셀의 기대빈도는 충분히 커서 근사 가정을 만족하므로 카이제곱 검정을 진행할 수 있습니다.
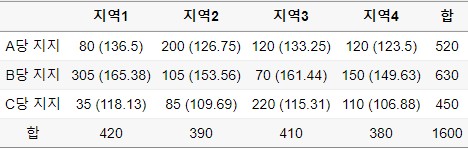
위에서 말씀드렸듯이, 기대빈도는 두 변수가 독립이라는 가정하에 구해진 빈도이므로 실제 관측빈도와 기대빈도의 차이가 크다는 것은두 변수의 연관성 역시 크다는 것을 의미합니다. 이 아이디어를 기반으로 각 셀에서의 관측빈도와 기대빈도의 총량을 이용하면 두 변수의 독립성을 판단할 수 있을 것입니다. 단순히 차이를 합치게되면 + / - 가 상쇄되므로 제곱을 해서 합치고 이는 카이제곱분포를 따르게 됩니다. 해당 식을 일반화하면 다음과 같습니다. \[ Q = \sum_{i=1}^a \sum_{j=1}^b \frac {(O_{ij}-E_{ij})^2} {E_{ij}} \; \sim \; \chi^2 (\;(a-1)(b-1)\;)\\ \]
\[ O : observed \; frequencies \qquad E : expected \;frequencies\\ \]
\[ a : number\; of\; categories\; for \; column \; variables\\ b: number\; of\; categories\; for\; row \; variables \]
구해진 검정통계량 Q는 자유도가 (열 변수의 범주 - 1) \(\cdot\) (행 범주의 범주 - 1) 인 카이제곱 분포를 따릅니다. 만약 Q가 크지 않다면 실제 관측빈도와 독립일 때의 기대빈도의 차가 전체적으로 크지 않다는 것을 의미하고 두 변수가 독립이라는 귀무가설을 기각하지 못할 것입니다. 반대로 Q 가 매우 크다면 두 변수는 연관성이 있다는 것을 의미하고 귀무가설을 기각하게 될 것입니다.
자유도가 저런 형태를 띠는 이유는 전체 표본 수 \(n\)이 고정되어있기 때문입니다. n이 고정된 상태로 기대빈도를 추정하면서 행의 합=\(n\), 열의 합=\(n\)이라는 제약식을 갖게 되고 그 조합으로 구해지는 Q는 (열 변수의 범주 - 1) \(\cdot\) (행 범주의 범주 - 1) 라는 자유도를 갖게 되는 것입니다.
이 방법을 이용하여 지역과 지지 정당이 독립인지에 대한 카이제곱 검정통계량을 구해보면 Q는 약 411.35가 되고 자유도는 (3-1)(4-1) = 6 이 됩니다. 이 경우 \(p-value\)는 매우 작아 두 변수가 독립이라는 귀무가설은 기각됩니다.
3. 카이제곱 독립성 검정(R Code)
카이제곱 독립성 검정은 분할표를 만든 후에 분석을 진행합니다. 인사관리 데이터(HR)를 통해서 분석을 진행하겠습니다.
left(이직 여부)와 salary(연봉 수준) 변수 간에 연관이 있는지 통계적으로 검정하고자 합니다. \[ H_0:이직\;여부와\;연봉 수준은\; 독립이다.\\ H_1:이직\;여부와\;연봉 수준은\; 독립이\;아니다.\\ \]
library(gmodels)
HR = read.csv("F:\\Dropbox\\DATA SET(Dropbox)//HR_comma_sep.csv")
HR$salary = factor(HR$salary ,levels = c('low','medium','high'))
CrossTable(HR$left,HR$salary,
prop.r = FALSE,prop.c = FALSE,prop.t = FALSE,
chisq = TRUE,expected = TRUE)
Cell Contents
|-------------------------|
| N |
| Expected N |
| Chi-square contribution |
|-------------------------|
Total Observations in Table: 14999
| HR$salary
HR$left | low | medium | high | Row Total |
-------------|-----------|-----------|-----------|-----------|
0 | 5144 | 5129 | 1155 | 11428 |
| 5574.188 | 4911.320 | 942.492 | |
| 33.200 | 9.648 | 47.915 | |
-------------|-----------|-----------|-----------|-----------|
1 | 2172 | 1317 | 82 | 3571 |
| 1741.812 | 1534.680 | 294.508 | |
| 106.247 | 30.876 | 153.339 | |
-------------|-----------|-----------|-----------|-----------|
Column Total | 7316 | 6446 | 1237 | 14999 |
-------------|-----------|-----------|-----------|-----------|
Statistics for All Table Factors
Pearson's Chi-squared test
------------------------------------------------------------
Chi^2 = 381.225 d.f. = 2 p = 1.652087e-83
카이제곱 독립성 검정을 진행하기 위해 분할표를 만들었습니다. 분할표를 만드는 명령어는 CrossTable()을 사용합니다.
prop.r, prop.t, prop.c는 각 셀에다 비율을 표시하는 것에 대한 옵션입니다. 만약 FALSE가 아닌 TRUE를 쓰면 분할표에서 비율이 표시 됩니다. 또한 chisq = TRUE는 카이제곱 독립성 검정을 실행하겠다는 옵션이고, expected = TRUE는 기대빈도를 표시하겠다는 옵션입니다.
카이제곱 검정 결과는 마지막에 Pearsons’s Chi-squared test에서 확인할 수 있습니다.
검정통계량 값인 Q는 Chi^2 = 381.225입니다.
\[ Q = \sum_{i=1}^a \sum_{j=1}^b \frac {(O_{ij}-E_{ij})^2} {E_{ij}}\\ \]
4. 로지스틱 회귀분석
로지스틱 회귀분석(logistic regression analysis)은 일반화 선형모형(generalized linear model, GLM)이라 불리는 큰 범주의 통계모형 모델링 방법에 속하는 방법입니다. 우선 GLM의 특징만 간단히 훑어보고 로지스틱 회귀모형에 대해 다루겠습니다.
GLM(Generalized Linear Model)
GLM은 문자 그대로 선형적이지 않은 대상(비선형)을 선형적으로 ’일반화’시킨 모형입니다.
선형화 시키는 이유는 여러 가지가 있을 수 있지만, 가장 대표적으로 선형모형에서만 사용할 수 있는 모형의 해석, 확장, 수정 등의 방법을 사용하기 위해서입니다.
비선형모형의 경우는 모형을 다루는 방법이 많이 제한될 뿐만 아니라 새로운 데이터에 민감하기 때문에 선형모형에 비해 덜 선호되는 경향이 있습니다.
그렇다면 로지스틱 회귀분석에서 선형화 시키는 대상은 무엇일까요? 바로 관심 범주에 속할 확률입니다. 확률은 일반적으로 예측자들에 따라 비선형하게 분포되어 있고, 형태는 S자 형태가 되는 경우가 많습니다. 물론 처음부터 확률에 선형라인을 적합시켜 선형회귀분석을 진행할 수도 있지만 이는 몇 가지 제약이 따릅니다.
library(ggplot2)
k = runif(n = 500,min = 2 , max = 4)
K = c()
P = c()
P1 = c()
for(i in k){
p1 = exp(-21.3 + 6.74*i) /(1 + exp(-21.3 + 6.74*i))
# error = runif(n = 1, min = -0.1, max = 0.1)
error = 0
p = p1 + error
p = ifelse(p < 0 ,0,p)
p = ifelse(p > 1, 1,p)
K = c(K,i)
P = c(P,p)
P1 = c(P1,p1)
}ggplot(NULL) +
geom_point(aes(x = K, y = P),col = 'royalblue', alpha = 0.2) +
theme_bw() +
scale_x_continuous(breaks = seq(2,4,by = 0.5)) +
xlab("Predictor") + ylab("Prob")위 그래프는 어떤 연속형 예측자에 따른 관심범주에 속할 확률입니다. 예를 들어 알콜 섭취량과 비만일 확률은 이런 식으로 분포할 수 있습니다. 알콜 섭취가 많을 수록 비만일 확률은 높아지지만 완전 선형적이라기 보다는 약간의 커브가 존재하는 것입니다. 우선여기에 일반적인 선형회귀 라인을 적합시켜 보겠습니다.
ggplot(NULL) +
geom_point(aes(x = K, y = P),col = 'royalblue', alpha = 0.2) +
geom_smooth(aes(x = K, y = P),method = 'lm', col = 'grey20') +
geom_hline(yintercept = c(0,1), linetype = 'dashed') +
scale_x_continuous(breaks = seq(2,4,by = 0.5)) +
theme_bw() +
xlab("Predictor") + ylab("Prob")선형 회귀선이 아주 비합리적이진 않습니다. 연속형 예측자가 증가함에 따라 확률 역시 증가하기 때문이죠. 또한 이런 선형식의 경우 위에서 배운 분산분석을 통한 모형의 적합도 검정부터 시작해서 기존에 회귀분석에서 사용하던 모든 분석을 진행할 수 있습니다. 그렇지만 이런 경우에는 구조적인 문제가 발생합니다. 바로 확률은 0과1 사이의 값을 갖는 데 반해 회귀선은 경우에 따라 음의 값이나 1을 초과하는 예측값를 제시할 수도 있다는 것입니다. 영역을 표시하자면 아래 동그라미와 같은 구간입니다.
ggplot(NULL) +
geom_point(aes(x = K, y = P),col = 'royalblue', alpha = 0.2) +
geom_smooth(aes(x = K, y = P),method = 'lm', col = 'grey20') +
geom_hline(yintercept = c(0,1), linetype = 'dashed') +
geom_point(aes(x = c(2.25,3.9), y = c(-0.05,1.05)),size = 10,shape = 1, col = 'red') +
scale_x_continuous(breaks = seq(2,4,by = 0.5)) +
theme_bw() +
xlab("Predictor") + ylab("Prob")세로축은 확률 값을 표현한 것인데, 빨간 동그라미는 확률이 가질 수 없는 값을 추정하고 있습니다. 위 데이터에서는 -4 이하의 점에서 -확률 값으로 추정되고 있지만, 이 회귀선을 이용하여 새 데이터를 예측해 보면 이보다 훨씬 많은 포인트가 잘못된 값으로 추정될 가능성이 있습니다. 또한 이러한 구조적인 문제로 확률의 특성을 이용한 기타 추가 분석 역시 불가능하게 됩니다.
그렇다면 이제 비선형적인 모형을 적합시켜보겠습니다. 아래 그래프는 S자 형태를 띠는 비선형적인 회귀곡선입니다.
ggplot(NULL) +
geom_point(aes(x = K, y = P),col = 'royalblue', alpha = 0.2) +
geom_line(aes(x = K, y = P1),col = 'red', size = 2.5, alpha = 0.5) +
geom_hline(yintercept = c(0,1), linetype = 'dashed') +
scale_x_continuous(breaks = seq(2,4,by = 0.5)) +
theme_bw() +
xlab("Predictor") + ylab("Prob")한눈에 보기에도 선형회귀선보다는 훨씬 데이터에 잘 적용됨을 알 수 있고 구조적인 문제도 발생하지 않습니다. 그렇지만 위에서 말씀드린대로 비선형 모델은 여러 가지 추가 분석에 제약이 있습니다. 이러한 제약을 극복하기 위해서 약간의 변환을 통해 이를 선형화하는 것이 로지스틱 회귀분석의 기본 아이디어입니다.
예측자가 주어졌을 때, 관심범주에 속할 확률을 선형으로 예측하기 이해서는 \(0 \leq \pi_x \leq1\)의 제약을 \(-\infty<log(\frac{\pi_x}{1-\pi_x})<\infty\)의 형태로 변환을 해주어야 합니다. \(\pi_x\)를 \(\frac{\pi_x}{1-\pi_x}\)로 변환, 즉 \(odds\)로 변환을 해주면, \(\frac{\pi_x}{1-\pi_x}\)는 \(0 < \frac{\pi_x}{1-\pi_x}<\infty\)의 범위를 가지게 됩니다. 그 후 \(log\)변환을 취해주면, 로그 함수의 특성에 따라 \(-\infty<log(\frac{\pi_x}{1-\pi_x})<\infty\)의 범위를 가지게 되는 것입니다. 우리는 관심범주의 확률을 선형모형으로 예측하기 위해 순수 \(\pi_x\)를 활용하는 것이 아니라, \(log(\frac{\pi_x}{1-\pi_x})\)를 활용할 것입니다. 이 변환을 \(logit\)변환이라 부르며, \(logit\)변환 값을 반응변수롤 하고 선형모델을 적합시킨 것을 로지스틱회귀분석이라고 합니다.
선형화를 위해 아래의 식을 고려해보겠습니다. 여기서 \(\pi_x\)는 설명 예측자가 주어졌을 때의 관심 범주에 속할 확률입니다.
\[ \pi_x = \frac {exp(\beta_0 + \beta_1 x )} {1+exp(\beta_0 + \beta_1 x )} \]
이는 일반 선형회귀에서의 \(\pi_x = \beta_0 + \beta_1 x\) 와 같이 직선의 관계를 나타내는 함수에 대응하는 것으로, 선형적인 관계가 아닌 성공확률 \(\pi_x\) 와 설명 예측자와의 관계를 S자 모양으로 표현해주는 함수입니다. 또한 선형화를 위해 위의 함수를 이용하여 선형식 모양으로 정리를하면 다음과 같습니다.
\[ logit(\pi_x) = log \left( \frac {\pi_x} {1-\pi_x} \right) = \beta_0 +\beta_1x \]
\(log \left(\frac{\pi_x}{1-\pi_x} \right)\) 와 같은 형태를 \(\pi_x\) 에 대한 로짓함수라고 부르며 \(logit(\pi_x)\) 와 같이 표현합니다. 이 로짓함수를 이용하면 우변을 선형식으로 표현할 수 있습니다. 이것이 처음에 말씀드렸던 확률과 예측자의 비선형적 관계를 선형식으로 일반화하는 과정입니다. 또한 로지스틱 회귀모형과 같은 GLM에서는 절편과 기울기를 일반적인 회귀분석과 다르게 최소제곱 추정법이 아닌 최대가능도도추정법(method of maximum likelihood estimation)이라 불리는 방법에 의해 추정합니다. 이는 다음 장에서 다루겠습니다
이제 구체적으로 로지스틱 모형을 살펴봅시다.
기본적인 로지스틱 모형은 반응 값이 이항변수임을 가정합니다. 잘 생각해보면, 위에서 계속 다루었던 확률은 주어진 값이 될 수 없다는 것을 떠올리실 수 있을 겁니다. 확률은 측정될 수 있는 것이 아니기 때문이죠. 설명을 위해 보여드린 그래프의 확률 값 역시 마찬가지입니다.
로지스틱 모형에서의 확률은 이항 반응 값으로 측정된 질적 자료를 이용해 추정됩니다. 예를 들어 알콜 섭취량과 비만일 확률의 관계를 알기 위한 조사를 할 때, ‘비만일 확률’ 자체는 측정할 수 없고 ‘비만 여부’ 라는 이항 반응 값을 측정해 그 확률을 추정한다는 것이죠.
이런 이항 반응 값(관심 범주 = 1)와 예측자간의 산점도를 그리면 다음과 같습니다.
PG = ifelse(P1 < 0.5,0, 1)
K1 = K + runif(n = length(K),min = -0.5, max = 0.5)
ggplot(NULL) +
geom_point(aes(x = K1, y = PG),col = 'royalblue') +
geom_line(aes(x = K, y = P1),col = 'red', size = 2.5, alpha = 0.5) +
theme_bw() +
xlab("Predictor") + ylab("Prob") +
scale_x_continuous(breaks = seq(2,4,by = 0.5)) 관심범주 아니면 비 관심범주로 조사된 세로 축 반응 변수는 0아니면 1의 값만 갖습니다. 관심있는 범주면 1을 부여하고 그렇지 않으면 0을 부여해 구별해 놓은 것이지요. 그에 비해 예측자는 연속적으로 분포함을 알 수 있습니다. 산점도를 보면 직관적으로 예측자 값이 큰 값을 가지면 관심범주에 속할 확률이 크고 작으면 비 관심 범주에 속할 확률이 크다는 것을 확인할 수 있습니다. 문제는 예측자가 겹치는 부분입니다. 하늘색 선을 기준으로 가장 왼쪽, 오른쪽 영역은 겹치는 부분이 없어 어렵지 않게 범주를 예측할 수 있지만 두 범주가 공존하는 가운데 부분은 예측자가 겹치게됩니다. 이 부분이 확률을 추정하여 로지스틱 회귀곡선을 그렸을 경우 변곡점이 생기는 영역이고 추정된 확률이 0.5에 가까운 애매한 값으로 표현되는 곳입니다. 즉, 예측하기 어려운 영역이라고 할 수 있습니다. 로지스틱 회귀곡선을 적합시켜 보겠습니다.
ggplot(NULL) +
geom_point(aes(x = K1, y = PG),col = 'royalblue') +
geom_vline(xintercept = c(2.7,3.6),linetype = 'dashed', col = 'red') +
geom_text(aes(x = c(2,4), y = c(0.5,0.5)),label = c("비관심범주","관심 범주"),col = 'red',
size = 5) +
geom_text(aes(x = 3.1, y = 0.5), label = "공존", col = 'royalblue',
size = 5) +
theme_bw() +
xlab("") + ylab("") +
scale_x_continuous(breaks = seq(1,5,by = 0.5)) 이 적합된 회귀곡선은 다음과 같습니다. \[ \hat \pi_x = \frac {exp(-21.3+6.74x)} {1+exp(-21.3+6.74x)} \; \Leftrightarrow\; log\left( \frac {\hat \pi_x} {1-\hat \pi_x} \right) = -21.3+6.74x \]
선형적으로 추정된 \(logit(\hat \pi)\) 는 꼭 연속형 예측자뿐 아니라 범주형 예측자도 가능하고 혼합된 형태도 가능합니다. 또한 모형에 대한 해석은 선형적으로 바라보아도 상관은 없으나 로짓 값이 직관적이지 않아 일반적으로 오즈비를 통해 하게됩니다.
예를 들어 위 식에서 예측자의 기울기 6.74는 ’예측자가 한 단위(1) 증가했을 때의 성공할 오즈 ’가 됩니다. 이것은 두 모형의 차를 통해 확인할 수 있습니다.
예측자가 \(x\) 인 모형과 한 단위(1) 증가하여 \(x+1\) 인 모형의 차를 봅시다. 아래 식에서는 추정된 확률의 구별을 위해 예측자가 \(x\) 인 경우 \(\hat {\pi}_{x}\) , \(x+1\) 인 경우 \(\hat \pi_{x+1}\) 로 표현하겠습니다.
\[ \left[\; -21.3+6.74(x+1) \;\right] - \left[\; -21.3+6.74(x) \;\right] = 6.74\\ \]
\[ \\ \quad \\ \Leftrightarrow \; \left[log\left( \frac {\hat \pi_{x+1}} {1-\hat \pi_{x+1}} \right) \right]-\left[log\left( \frac {\hat \pi_x} {1-\hat \pi_x} \right) \right] =log \left[ \left(\frac {\hat \pi_{x+1}} {1-\hat \pi_{x+1}} \right)/\left( \frac {\hat \pi_x} {1-\hat \pi_x} \right)\right]= log(\widehat {o.r} ) \]
즉, 로지스틱 회귀모형에서의 기울기는 예측자가 1 증가했을 때의 로그오즈비 추정량이고 \(exp[기울기]\) 는 예측자가 한 단위 증가했을 때의 오즈비 추정량입니다. 위의 예에서 적용해보면 예측자가 한 단위 증가할 때 관심범주에 속할 오즈가 \(exp(6.74) = 846\) 배가 된다는 것을 알 수 있습니다. 이를 응용하면 단위를 조정해서 확인할 수도있습니다. 예를 들어 위에서 다룬 예제는 예측자의 범위가 매우 작으므로 1이 아닌 0.1이 증가했을 때의 오즈비를 확인하고 싶을 수 있습니다. 로그오즈비는 \(\left[\; -21.3+6.74(x+0.1) \;\right] - \left[\; -21.3+6.74(x) \;\right] = 0.674\) 이 되겠고 오즈는 \(exp(0.674)=1.96\) 이 됩니다. 즉, 예측자가 0.1 증가하면 관심 범주에 속할 오즈가 1.96배 됨을 알 수 있습니다.
5. 로지스틱 회귀분석(R Code)
로지스틱 회귀분석도 결국은 회귀분석이기에 돌리는 방법은 비슷하지만 일반적인 회귀분석보다는 좀 까다롭습니다. 데이터는 역시 인사관리 데이터(HR)를 이용하여 진행하겠습니다.
직원들의 이직 여부를 판단하는 분류 모형을 만들어 통계적으로 검정하고자 합니다.
\[ H_0:이직에\;영향을\;미치는 변수들의\;기울기는\;0이다.\\ H_1:not\;H_0 \]
로지스틱 회귀분석
Logistic = glm(left ~ satisfaction_level + salary + time_spend_company,
data = HR, family = binomial())로지스틱 회귀분석은 일반화 선형 모형이기 때문에 glm() 명령어로 진행합니다.
family = binomial()은 일반화 선형 모형에서는 다양한 분포의 종속 변수에 적용하기 때문에, 종속 변수가 어떤 분포를 따르고 있는지 옵션을 주는 것입니다. left는 이직 여부를 나타내는 이항 변수이므로 이항 분포를 따르고 있습니다. 그러므로 binomial()을 설정해줍니다.
summary(Logistic)Call:
glm(formula = left ~ satisfaction_level + salary + time_spend_company,
family = binomial(), data = HR)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.8628 -0.6774 -0.4666 -0.1781 2.7644
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.48069 0.07532 6.382 1.75e-10 ***
satisfaction_level -3.72386 0.08852 -42.069 < 2e-16 ***
salarymedium -0.53427 0.04436 -12.044 < 2e-16 ***
salaryhigh -1.98592 0.12461 -15.938 < 2e-16 ***
time_spend_company 0.21159 0.01418 14.922 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 16465 on 14998 degrees of freedom
Residual deviance: 13597 on 14994 degrees of freedom
AIC: 13607
Number of Fisher Scoring iterations: 5결과표 해석은 회귀분석에서 했던 것과 같습니다. 또한 Deviance, AIC 값은 다음 장에서 설명하도록 하겠습니다. 여기서 주목해야 되는 점은 Dummy variable(가변수)로 변환되어 모형에 투입 된 salary 변수의 기울기 해석입니다.
Dummy variable은 범주형 변수가 회귀 모형에 투입될 때 분석에 맞게 변환 된 변수입니다. 성별(Male, Female)변수를 회귀모형에 투입하기 위해 Dummy variable로 변환시켜 보겠습니다.

더미 변수 변환은 먼저 하나의 수준을 기준점(reference)으로 정하는 것부터 시작합니다. 여기 예시에서는 Male을 기준점으로 해서 Male일 때는 D_1이 0을 가지고 Female에 해당될 때는 1을 가지도록 변환했습니다. 이 변수를 모형에 투입하면 다음처럼 해석합니다.
\[ \hat{y_i}=b_0+b_1D_1 \] - Male 일 경우 : \(\hat{y_i}=b_0\)
- Female일 경우 : \(\hat{y_i}=b_0+b_1\)
Female일 경우 Male일 때보다 \(\hat{y_i}\)가 \(b_1\)만큼 증가한다는 의미를 가지고 있습니다. 이렇게 기준점을 기반으로 해석을 진행합니다. 다음으로는 salary 변수처럼 3가지 수준을 가지고 있을 때는 어떻게 진행하는지 보도록 하겠습니다.

R에서는 기본적으로 Factor 변수가 모형에 들어오면 자동으로 Dummy variable로 변환해서 결과값을 출력합니다. 기준점은 첫 번째로 인식된 수준입니다. 기준을 바꿔주고 싶다면 factor 지정을 해주시면 됩니다.
HR$salary = factor(HR$salary ,levels = c('low','medium','high'))분석 전에 위와 같은 명령어를 통해 salary 변수의 level 순서를 ‘low’, ‘medium’, ’high’순으로 지정 해줌으로써 low가 자동으로 기준점이 된 것입니다.
분석 결과 R에서 제시된 로지스틱 회귀식을 정리하면 다음과 같습니다.
\[ log(\frac{\hat{\pi}_x}{1-\hat{\pi}_x})=0.48-3.72\ Satisfaction\;level -0.53\ salarymedium\\ - 1.98\ salaryhigh+0.22\ time\;spend\;company \]
Dummy variable로 변환이 된 salary변수부터 해석해 보겠습니다.
\[ low:log\left(\frac{\hat{\pi}_x}{1-\hat{\pi}_x}\right)=0.48-3.72\ Satisfaction\;level-0 \\+0.22\ time\;spend\;company\\ \; \] \[ medium:log\left(\frac{\hat{\pi}_x}{1-\hat{\pi}_x}\right)=0.48-3.72\ Satisfaction\;level-0.53\\+0.22\ time\;spend\;company \] \[ high:log\left(\frac{\hat{\pi}_x}{1-\hat{\pi}_x}\right)=0.48-3.72\ Satisfaction\;-1.98\\+0.22\ time\;spend\;company \]
- 기준점인 low일 때는 medium & high에 해당되는 회귀 계수는 모두 0이 됩니다.
- medium일 때는 salarymedium의 회귀 계수인 \(-0.53\)이 남아 있어, logit값이 -0.53만큼 낮아집니다.
- high 집단에 속할 때는 low 집단에 비해 이직을 할 logit값이 \(-1.98\)만큼 감소합니다.
- 나머지 satisfaction_level은 증가할수록 이직할 logit은 내려가게 되고, \(time\ spend\ company\)는 증가할수록 이직할 logit은 증가하는 것을 의미합니다.
- 각 변수의 계수에 지수변환을 해주면 해당 변수의 변화에 따른 오즈비 역시 구할 수 있습니다.
모형의 성능 평가
회귀분석에서는 \(R^2\)를 통해 모형의 성능을 평가하지만, 일반적으로 로지스틱 회귀분석에서는 다른 방법을 사용하게 됩니다. 그 방법은 분류 모형이 실제로 얼마나 맞췄는가를 평가하는 것입니다. 그러기 위해서는 만들어진 로지스틱 회귀 모형에 데이터를 집어 넣어, 확률을 추정하고 그에 따른 분류를 해야합니다.
Log_odds = predict(Logistic, newdata = HR)
Probability = predict(Logistic, newdata = HR, type = 'response')- predict()는 만들어진 모형에 데이터를 넣어 추정값을 계산하는 방식입니다.
- type 옵션이 없으면 predict을 통해 \(log(\frac{\hat{\pi}_x}{1-\hat{\pi}_x})\)이 계산이 됩니다.
- type = ‘response’ 옵션을 주면 predict을 통해 \(\hat{\pi}_x\)가 계산이 됩니다. 즉, 우리가 관심이 있는 값은 직원들이 이직을 할 확률 \(\hat{\pi}_x\)이기에 옵션을 준 값으로 계산을 해야합니다.
그 다음으로는 계산된 \(\hat{\pi}_x\)를 가지고 이직 여부를 판단해야 됩니다. 예를 들어 이직 할 확률이 0.5보다 큰 경우에는 이직으로 판단, 나머지는 이직을 하지 않는 집단으로 분류 합니다. 여기서 확률을 구분 짓는 값을 cut-off value라고 합니다.
PREDICTED_C = ifelse(Probability > 0.5 , 1 , 0)
PREDICTED_C = factor(PREDICTED_C,levels = c(1,0))다음 처럼 ifelse()문을 이용하여 cut-off value에 따라 분류를 진행해줍니다. 그 다음으로는 실제 값과 모델에 의한 분류 결과를 비교해야합니다.
# install.packages(c("caret","e1071"))library(caret)
HR$left = factor(HR$left, levels = c(1,0))
confusionMatrix(PREDICTED_C,HR$left)Confusion Matrix and Statistics
Reference
Prediction 1 0
1 947 872
0 2624 10556
Accuracy : 0.7669
95% CI : (0.7601, 0.7737)
No Information Rate : 0.7619
P-Value [Acc > NIR] : 0.07635
Kappa : 0.2272
Mcnemar's Test P-Value : < 2e-16
Sensitivity : 0.26519
Specificity : 0.92370
Pos Pred Value : 0.52062
Neg Pred Value : 0.80091
Prevalence : 0.23808
Detection Rate : 0.06314
Detection Prevalence : 0.12127
Balanced Accuracy : 0.59444
'Positive' Class : 1
실제값과 모델에 의한 분류값을 비교하는 테이블을 Confusion Matrix라고 합니다.

- True Positive & True Negative는 모형 예측값이 실제 값을 맞춘 경우에 해당됩니다.
- False Negative & False Positive는 모형 예측값이 실제 값을 맞추지 못한 경우에 해당됩니다.
- Accuracy : \(\frac{TP+TN}{TP+FP+FN+TN}\) : 전체 정확도를 의미합니다.
- Sensitivity(민감도) : \(\frac{TP}{TP+FN}\) :실제 Positive 중에서 모형이 Positive를 맞추었는가에 대한 지표입니다.
- Specificity(특이도) : \(\frac{FP}{FP+TN}\) : 실제 Negative 중에서 모형이 Negative를 맞추었는가에 대한 지표입니다.
전체 정확도만 보는 것이 아니고 민감도 및 특이도를 보는 이유는 다음과 같습니다.
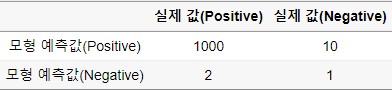
극단적인 결과지만, 분석을 잘못 돌린 경우 이러한 분석결과가 나올 때가 종종 있습니다. 이 분석 결과에 따르면 Accuracy는 98%로 매우 높습니다. 하지만 Specificiy는 0.1도 되지 않습니다. 이러한 분석 모형은 크게 의미가 없습니다. 모형이 데이터를 Neagtive로 분류하지 못하기 때문입니다.
각 산업군마다 중요한 부분이 다릅니다.
예를 들어 병원에서 환자의 질병을 판단하는 분류 모형을 만들어 해당 모형의 정확도를 계산하는 경우에, False Positive : 실제로 Negative인데 Positive로 오분류한 경우 (병이 없는데 병이 있다고 분류) False Negative : 실제로 Positive인데 Negative로 오분류한 경우 (병이 있는데 병이 없다고 분류) 질병을 발견 못하는 실수는 돌이킬 수가 없기에, 병원에서는 False Negative가 False Positive가 더 중요한 값일 수 있습니다.
Confusion Matrix의 결과를 통해 Accuracy, Sensitivity, Specificity의 값을 확인할 수가 있습니다. 여기서 하나 주의할 점은, 위에서 cut-off value를 0.5로 하여 분류했다는 것입니다. 이 cut-off value가 중요한 이유는 그 값에 따라 분류가 천차만별이기 때문입니다. 그렇기에 모든 cut-off value를 고려하여 결과값의 변화를 살펴봐야하는데, 그 방법을 ROC curve라고 합니다.
Roc Curve
library(pROC)
HR$left = factor(HR$left,levels = c(0,1))
ROC = roc(HR$left,Probability)
plot.roc(ROC,
col="royalblue",
print.auc=TRUE,
max.auc.polygon=TRUE,
print.thres=TRUE, print.thres.pch=19, print.thres.col = "red",
auc.polygon=TRUE, auc.polygon.col="#A0A0A0")Roc Curve의 y축은 Sensitivity이며, x 축은 Specificity입니다.
X축이 1 ~ 0 순서로 그려져 있는 것을 주의하시기 바랍니다.
Roc Curve는 cut off value의 값에 따라 Sensitivity와 Specificity의 변화량을 나타낸 그래프입니다.
AUC는 Area under curve의미로, 곡선에 해당되는 면적을 나타냅니다. AUC값이 높을수록 바람직한 모형이라고 할 수 있습니다.
가장 좋은 결과값을 나타내는 cut off value 값 및 sensitivity, specificity 역시 추가할 수 있습니다.
이렇게 로지스틱 회귀분석의 이론 및 실습방법을 다루었습니다. 분류모형은 이런 로지스틱 기법이 기본 아이디어이긴 하지만, 정확한 분석을 위해서는 Train / Test SET을 통한 타당성 검증, 좋은 변수 선택법 및 기계학습 알고리즘과의 비교 분석 등이 함께 되어야 합니다. 다음 장에서부터는 해당 내용을 다루도록 하겠습니다.
'MustLearning with R 1편' 카테고리의 다른 글
| 14. 기계학습 (1) | 2020.01.29 |
|---|---|
| 13. 기초통계 이론 3단계 (0) | 2020.01.29 |
| 11. 기초통계이론 2단계 (0) | 2020.01.29 |
| 10. 기초통계 이론 1단계 (1) | 2020.01.29 |
| 9. ggplot2를 활용한 다양한 그래프 그리기 (0) | 2020.01.29 |




